Example of Incompressible elasticity with mpm symbolic module

Mixed formulation for incompressible elasticity using MPM symbolic module

A formulation of the elasticity problem able to represent the incompressible behavior can be written using mixed approach involving pressure and displacement fields

\[\nabla p + 2\mu\nabla\cdot\rm{dev}[\nabla^s u]+f = 0\;\rm{in}\ \Omega\] \[\frac{1}{K}p-\nabla\cdot u=0\;\rm{in}\ \Omega\] \[u=\bar u\;\rm{on}\ \Gamma_u\] \[\sigma n = \bar t\;\rm{on}\ \Gamma_t\]

The weak form of the above equations can be written as \(\int_\Omega\overbrace{2\mu\nabla^sw:\rm{dev}[\nabla^su]}^{T_1}\ d\Omega-\int_\Omega\overbrace{ \nabla\cdot w\ p}^{T_2}\ d\Omega=\int_{\Gamma_t}\overbrace{w\cdot \bar t}^{T_3}\ d\Gamma\)

\[-\int_\Omega\underbrace{q\ \nabla\cdot u}_{T_4 = T_2^T}\ d\Omega+\int_\Omega\underbrace{\frac{1}{K}q\ p}_{T_5}\ d\Omega = 0\]

where

• $u, p$ are unknown displacement and pressure fields (Variables).
• $w, q$ are test fields (Variables) In order to obtain stable results, the approximations should satisfy Babuška-Brezzi condition or some form of stabilization would be required. To satisfy the B-B condition, the approximation order of displacement should be higher than that of hydrostatic pressure. In the following we will consider 2D case.

In the input deck, the Variables ($u,p,w,q$) can be set up using following syntax

Variable name "u" interpolation "feilin" type 1 quantity 0 size 2 dofs 2 1 2 
Variable name "w" interpolation "feilin" type 1 quantity 0 size 2 dofs 2 1 2 
Variable name "p" interpolation "feiconst"  type 0 quantity 3 size 1 dofs 1 11  
Variable name "q" interpolation "feiconst" type 0 quantity 3 size 1 dofs 1 11 

where interpolation determines the interpolation used for specific field. Here we use linear approximation (interpolation “feilin”) for displacement field and related test field and constant approximation (interpolation “feiconst”) for pressure (so called Q1P0 element). The $u, w$ fields are vector fields (type 1) with physical meaning of displacement (quantity 0) and two degrees of freedom (size 2 dofs 2 1 2). And $p, q$ are scalar fields (type 0) with physical meaning of pressure (quantity 3 size 1 dofs 1 11).

The weak form above consists of several terms to be evaluated

• $T_1$: This is represented by BTSigmaTerm, evaluated for $w$ test field and $u$ as unknown field, under plain strain assumptions (mmode 7) and considering deviatoric part only (lhsmatmode 29)

  BTSigmaTerm 1 variable "u"  testvariable "w" mmode 7 lhsmatmode 29
  

• $T_2$: represented by BTamNTerm, evaluated for $w$ test field and $u$ as unknown field, under plain strain assumptions (mmode 7) and with scalar parameter equal to 1.0 (atype 28)

  BTamNTerm 2 variable "p" testvariable "w" mmode 7 atype 28
  

• Similarly, we set up remaining three terms $T_3, T_4=T_2^T$ and $T_5$:

  NTamTBTerm 3 variable "u" testvariable "q" mmode 7 atype 28
  NTcN 4 variable "p" testvariable "q" mmode 7 ctype 27
  NTfTerm 5 variable "u" testvariable "w" mmode 6 flux 2 0. 6.25
  

  The terms are integrated over specific domains ($\Omega,\ \Gamma_t$), defined using corresponding sets (defined bellow in the example):

  Integral 1 domain 1 set 1 term 1
  Integral 2 domain 1 set 1 term 2 factor -1.0
  Integral 3 domain 1 set 1 term 3 factor -1.0
  Integral 4 domain 1 set 1 term 4 factor -1.0
  Integral 5 domain 1 set 2 term 5
  

  Example: Cook membrane

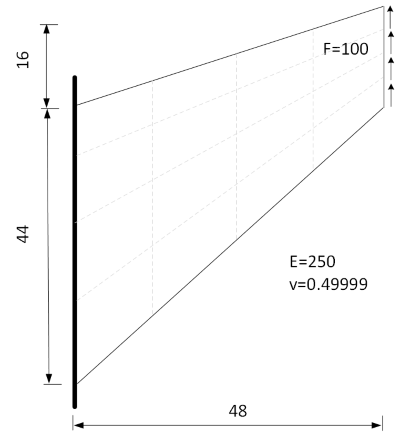
  The Cook’s membrane is a standard benchmark problem. It consists of a tapered plate clamped on one of its sides with a transversal distributed load applied to the opposite side. The plate is in plain strain and its dimensions, as well as the material parameters and boundary conditions, are shown in figure bellow

The complete OOFEM input deck for mesh consisting of 2x2 is shown below

cook2.out
Demo of symbolic mpm problem; Cook membrane benchmark
# 
test nsteps 1 nvariables 4 nterms 5 nintegrals 5 lhsterms 4 1 2 3 4 rhsterms 1 5
Variable name "u" interpolation "feilin" type 1 quantity 0 size 2 dofs 2 1 2 # displacement 
Variable name "w" interpolation "feilin" type 1 quantity 0 size 2 dofs 2 1 2 # test function
Variable name "p" interpolation "feiconst"  type 0 quantity 3 size 1 dofs 1 11 # pressure 
Variable name "q" interpolation "feiconst" type 0 quantity 3 size 1 dofs 1 11 # test function
BTSigmaTerm 1 variable "u"  testvariable "w" mmode 7 lhsmatmode 29
BTamNTerm 2 variable "p" testvariable "w" mmode 7 atype 28
NTamTBTerm 3 variable "u" testvariable "q" mmode 7 atype 28
NTcN 4 variable "p" testvariable "q" mmode 7 ctype 27
NTfTerm 5 variable "u" testvariable "w" mmode 6 flux 2 0. 6.25
#NTfTerm 5 variable "u" testvariable "w" mmode 6 flux 2 0. 31.25
Integral 1 domain 1 set 1 term 1
Integral 2 domain 1 set 1 term 2 factor -1.0
Integral 3 domain 1 set 1 term 3 factor -1.0
Integral 4 domain 1 set 1 term 4 factor -1.0
Integral 5 domain 1 set 2 term 5
domain HeatTransfer
outputmanager tstep_all dofman_all element_all
ndofman 9 nelem 6 nbc 1 ncrosssect 1 nic 0 nltf 2 nmat 1 nset 3
Node 1 coords 3 0.0 0.0 0.0
Node 2 coords 3 24.0 22.0 0.0
Node 3 coords 3 48.0 44.0 0.0
Node 4 coords 3 0.0 22.0 0.0
Node 5 coords 3 24.0 37.0 0.0
Node 6 coords 3 48.0 52.0 0.0
Node 7 coords 3 0.0 44.0 0.0
Node 8 coords 3 24.0 52.0 0.0
Node 9 coords 3 48.0 60.0 0.0
q1 1 nodes 4 1 2 5 4 mat 1 crosssect 1
q1 2 nodes 4 2 3 6 5 mat 1 crosssect 1
q1 3 nodes 4 4 5 8 7 mat 1 crosssect 1
q1 4 nodes 4 5 6 9 8 mat 1 crosssect 1
l1 5 nodes 2 3 6 mat 1 crosssect 1
l1 6 nodes 2 6 9 mat 1 crosssect 1
simplecs 1 thick 5.0
isole 1 d 1 e 250 n 0.49999 talpha 1.
# clamped-displacement
boundarycondition 1 loadtimefunction 1 set 3 values 2 0 0   dofs 2 1 2
constantfunction 1 f(t) 1
PiecewiseLinFunction 2 nPoints 4 t 4 -10. 0. 1. 5. f(t) 4 0. 0. 1.0 1.0
set 1 elementranges  {(1 4)}
set 2 elementranges  {(5 6)}
set 3 elementedges 4 1 4 3 4

The complete input deck can be found in tests/mpm/cook2_u1p0.in file.

Switching to high-order interpolation

To switch to high order element Q2P1 with quadratic interpolation of displacement and linear interpolation of pressure we need just to use different interpolations for variables. The updated variable input records are following

Variable name "u" interpolation "feiquad" type 1 quantity 0 size 2 dofs 2 1 2 # displacement 
Variable name "w" interpolation "feiquad" type 1 quantity 0 size 2 dofs 2 1 2 # test function
Variable name "p" interpolation "feilin"  type 0 quantity 3 size 1 dofs 1 11 # pressure 
Variable name "q" interpolation "feilin" type 0 quantity 3 size 1 dofs 1 11 # test function

The complete input deck can be found in tests/mpm/cook2_u2p1.in file.

Note: At the time of writing, the oofem version from mpm2 branch is required to run the example.

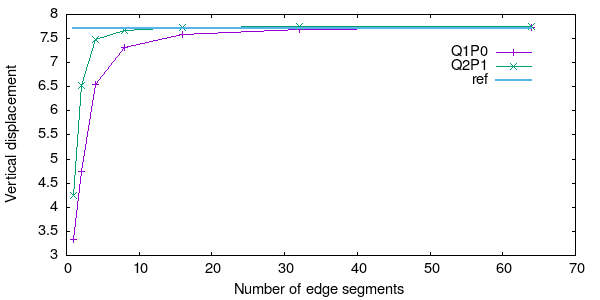
To illustrate the convergence, sequence of uniform meshes of the plate is considered, starting from a mesh consisting of a single elements and proceeding by uniform refinement.

The figure below shows the vertical displacement of the plane tip plotted against the number of element segments along each side. The solution is compared to reference solution ¹.

With this I conclude today post on mpm module. Hope you enjoyed and stay tuned for following updates!

You are welcome to leave a comment below to give a feedback.

References

1. Ignacio Romero, Manfred Bischoff, Incompatible Bubbles: A non-conforming finite element formulation for linear elasticity, Computer Methods in Applied Mechanics and Engineering, Volume 196, Issues 9–12, 2007, Pages 1662-1672, ISSN 0045-7825, https://doi.org/10.1016/j.cma.2006.09.010. ↩